Building an OFDM Modem that Operates in the Audio Spectrum Part 2 #
Resources #
-
Part 2 Video
Part 2 Goals/Requirements #
✅ Tx: digital to analog conversion, aka get our speaker playing our OFDM symbols
✅ Implement OFDM preambles
✅ Write the following blocks in the receiver processing chain:
- timing synchronization (based off preambels)
- cyclic prefix removal
- fft/generalized receive symbols block
✅ Write functionality to receive OFDM symbols in the audio spectrum with configurable:
- baseband sampling rate
- transmit sampling rate
- transmit center frequency
Transmitting via Sound #
In part 1, we wrote the code to generate time-domain OFDM symbols modulated data input to an IFFT. Now, we need to add functionality to the tinyofdm class to get those samples out of our speakers.
To do this, the python library sounddevice is used. sounddevice allows for us to pass our numpy arrays directly to the play method. We can record numpy arrays from our microphone with the rec method. In later section we will work on real-time i/o, but for getting started we simply just want to play our symbols out of our speakers with play. usage:
sd.play(data, self.fs_tx)
The OFDM Receiver #
After passing through the channel it is the OFDM receivers job to correct for unideal characteristics in the received signal. Some important aspects of proper reception include: synchronization (which includes packet detection, timing recovery, and carrier frequency offset correction) and channel equalization. The general flow of what we will implement in part 2 is summarized in the figure below.
scroll---->
+-----------------+ +-----------------+ +-----------------+ +-----------------+ +-----------------+ +-----------------+ +-----------------+
| | | | | | | | |[NOT IMPLEMENTED]| | | | |
| | | | | | | | | CARRIER FREQ. | | | | |
| MICROPHONE |---------> FREQUENCY SHIFT |--------->| DECIMATION TO |--------->| TIMING |--------->| OFFSET |--------->| CYCLIC PREFIX |--------->| FFT |
| | | | | FS BASEBAND | | SYNCHRONIZATION | | CORRECTION | | REMOVAL | | |
| | | | | | | | | | | | | |
+-----------------+ +-----------------+ +-----------------+ +-----------------+ +-----------------+ +-----------------+ +-----------------+
Part 2 of this build will only touch on packet detection/timing recovery. Carrier frequency offset correction (CFO) and channel equalization will be in part 3. Since CFO and equalization are more complex phenomena we can do loop-back tests to test the tx-rx without these blocks for now.
Packet Detection and OFDM Preambles #
The first step to synchronization is packet detection, which deals with finding the start of an OFDM transmission. Various detection techniques have been proposed and implemented in 802.11 systems but the seminal work laid out by [1] for packet detection proves to be, as the title states, a truly robust solution to detection. However, unlike the packet structure proposed in [1], the implementation of OFDM in tinyofdm adheres closely the 802.11p standard which uses a special series of training sequences called the short preamble and long preamble. The short and long preamble make up the IEEE 802.11 PLCP preamble [2] as shown below
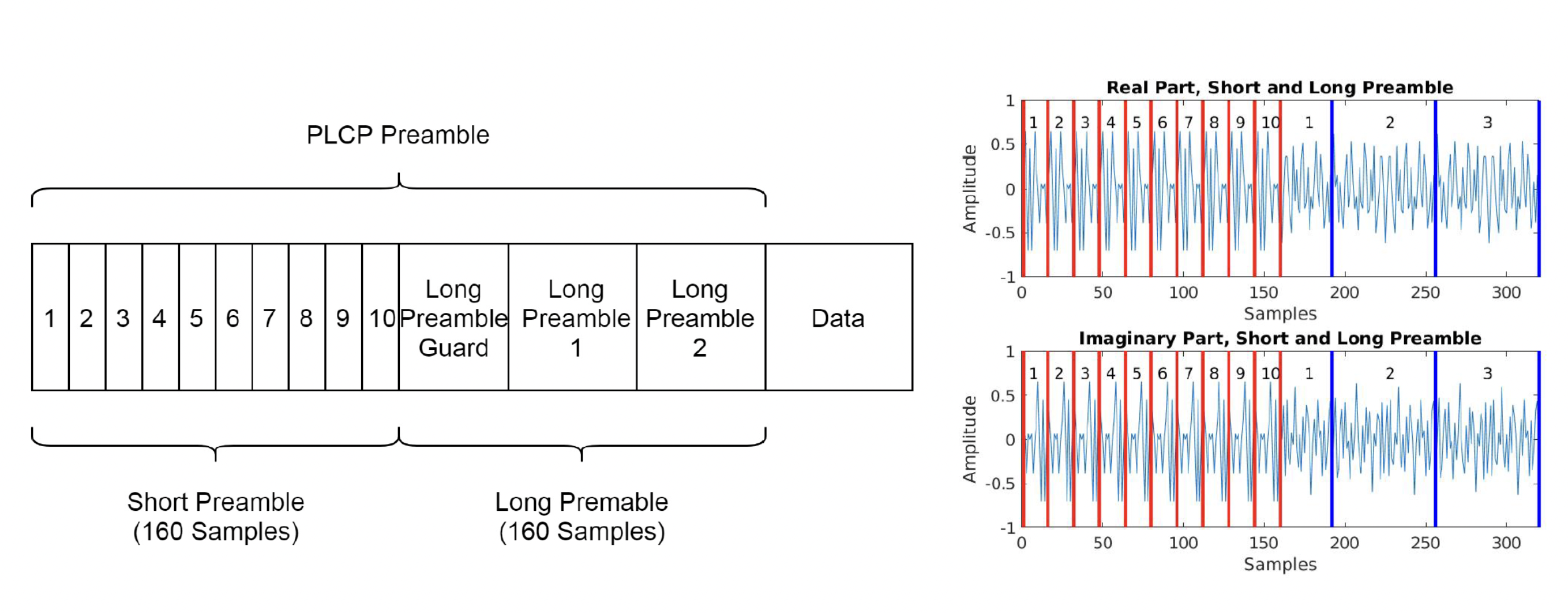
An OFDM frame begins with a 160-sample length preamble that is constructed such that there exists 10 identical short training symbols of duration \(\frac{160}{10} T_s\). In the tinyofdm implementation, for example, 4KHz of bandwidth is used, this works out to be 4ms in duration for each repetition or 40ms in total. The short training symbol is used for signal detection, coarse frequency offset, and may be used for timing synchronization as well [2]. The detection method employed by the OFDM modem implemented in tinyofdm follows the metric proposed in [1] and is characterized in belows. The method takes advantage of the short preambles repetitive nature by calculating correlation of the incoming signal,srx, with the signal \(L\) samples later as:
$$C[n] = \sum_{m=0}^{L-1} s_{rx}^*[n+m] \cdot s_{rx}[n+m+L]$$
Where \(L\) is typically the length of the repeating pattern (in implementation \(L = 16\) samples long). The energy of the incoming signal is then calculated in a window of \(L\):
$$P[n] = \sum_{m=0}^{L-1} | s_{rx}[n+m_L]|^2$$
The two terms are combined in the M(n) metric, which is then the correlation scaled by the energy as:
$$M[n] = \frac{|C[n]|^2}{P[n]^2}$$
The nature of the \(M[n]\) metric is advantageous as the it will settle close to 1 as the short preamble moves through the processing delay lines, as seen in the figure below.
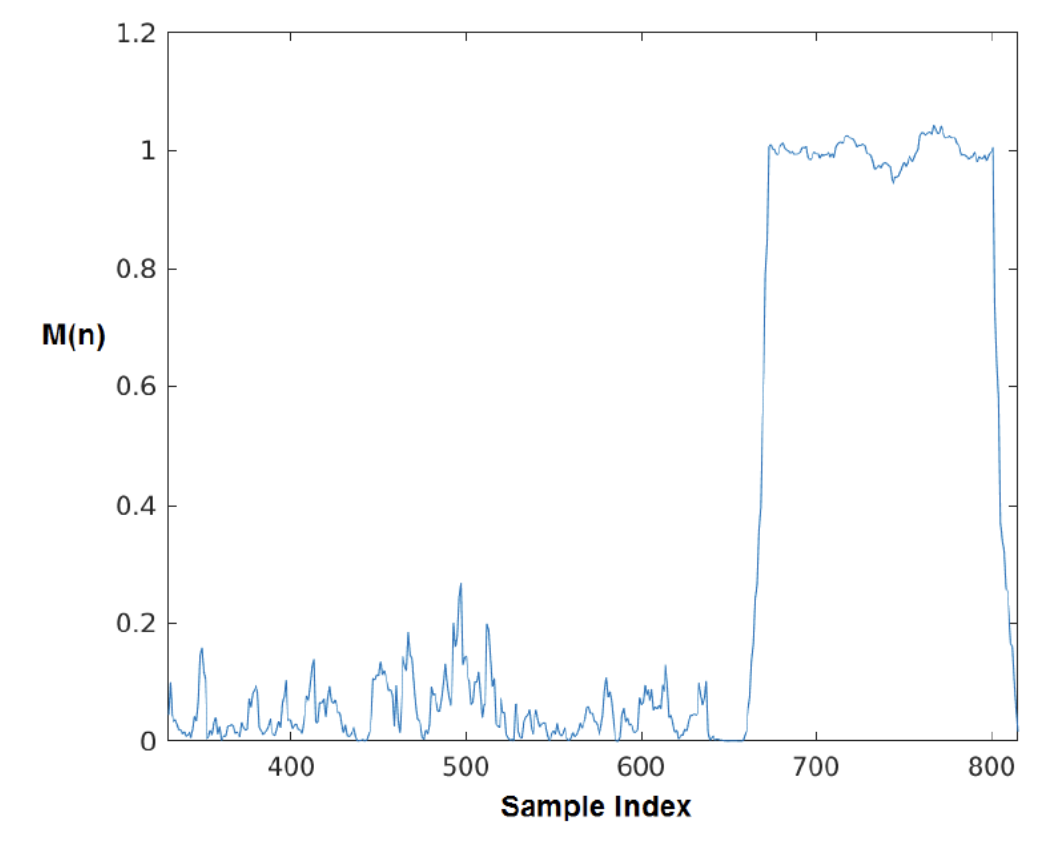
The correlation will last for \(160 − 2 \cdot L\) samples as the symbols need to propagate through two delay windows of size L before packet detection settles near 1. For example with \(L = 16\), this means that the first correlation close to 1 will occur 32 samples into the short preamble and last 128 samples thereafter. Waiting L samples above a certain threshold (0.8 proves to work well) before issuing a packet detection signal ensures the correlation is due to the short preamble and not spurious events or another periodic signal.
References #
[1] T. M. Schmidl and D. C. Cox, “Robust frequency and timing synchronization for ofdm,” IEEE Transactions on Communications, vol. 45, no. 12, pp. 1613–1621, Dec 1997.
[1] G. Maier, A. Paier, and C. F. Mecklenbruker, “Packet detection and frequency synchronization with antenna diversity for ieee 802.11p based on real-world measurements,” in 2011 International ITG Workshop on Smart Antennas, Feb 2011, pp.1–7.