HardwareTeams.com - The #1 job board and blog for electrical and computer engineers

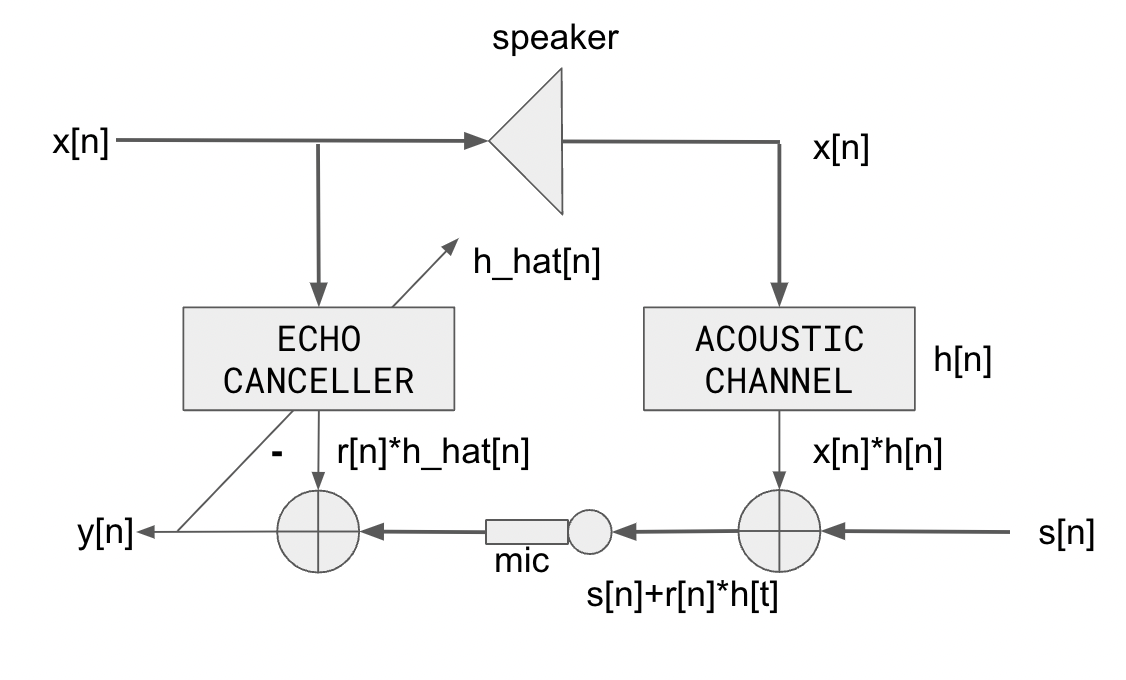
Acoustic Echo Cancellation Using the LMS algorithm #

This code covers: Adaptive algorithms with an automatic gain control feature (The Least Mean Squares part - section II of the IEEE paper)

Acoustic echo cancellation (AEC) is a crucial technology used in communication systems to eliminate unwanted echoes that can degrade audio quality. One popular and widely used algorithm for AEC is the Least Mean Squares (LMS) algorithm. The LMS algorithm is a adaptive filter-based approach that can effectively estimate and remove acoustic echoes in real-time, making it ideal for applications such as teleconferencing, voice-over-IP (VoIP) systems, and hands-free communication.

Implement this circuit

acous-echo

Papers #

IEEE Paper

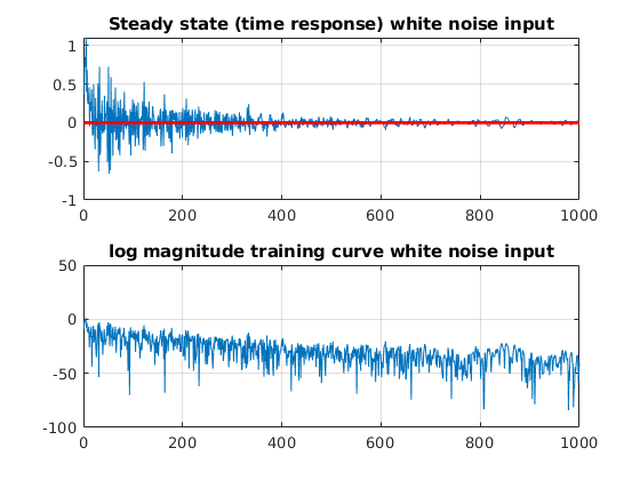
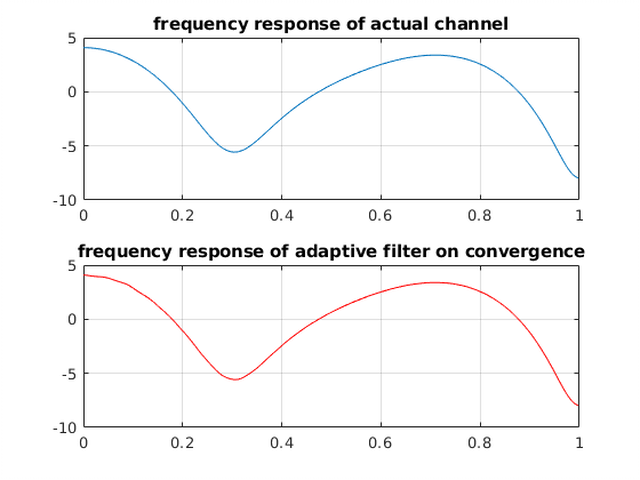
Results From Code Below #

Code #

clear all;
close all;

%channel
num = [1 0 0 0.5 0 .1];
den = [1 0 0  0 0 0];

[Hc,Wc] = freqz(num,den);
tmax = 10000;

trainlen = tmax;


%training signal
x = 1*rand(1,tmax);

%desired signal
s_t = 0;

%signal through channel
x_ht = filter(num,den,x);

%signal through channel + desired
mic_in = s_t + x_ht;

%50-length adaptive filter
reg1=zeros(1,50);
wts = (zeros(1,50));

%mu for LMS algorithm
mu  = .055;

%run LMS on signal
for n = 1:trainlen

  reg1 = [x(n) reg1(1:49)];

  err = mic_in(n) - reg1*(wts');

  y(n) = err;

  wts = wts + mu*(reg1*(err'));

end


figure
subplot(211)
plot(1:length(y(1:1000)), (y(1:1000)))
hold on
plot(1:1000, zeros(1,1000), 'color', 'r', 'linewidth', 2, 'MarkerSize', 2)
hold off
axis([ -.5 1000 -1 1.1])
grid on
title('Steady state (time response) white noise input')
subplot(212)
plot(1:length(y(1:1000)), 20*log10(abs(y(1:1000)) ))
grid on
title('log magnitude training curve white noise input')

[Hf,Wf] = freqz(wts);
figure
subplot(211)
plot(Wc/pi, 20*log10(abs(Hc)))
grid on
title('frequency response of actual channel')
subplot(212)
plot(Wf/pi, 20*log10(abs(Hf)),'color','r')
title('frequency response of adaptive filter on convergence')
grid on