FIR Filter Design and Verification with Python and Cocotb #
Intro #
In the getting started tutorial we implemented a basic verilog module and simulated it with iverilog and cocotb. This tutorial will be a DSP focused look at cocotb.
What this tutorial is about #
In this tutorial we will:
- design a filter in python using numpy and scipy
- translate that design to verilog
- verify verilog implementaiton of our filter with cocotb
Design the FIR #
We need to design some filter taps to put into our verilog design, so lets do that. Lets say our filter has the following requirements:
- a passband of
+/- 0.1 * Fs - a transition of
0.1 * Fs - must be length 13
filter_design.py #
import matplotlib.pyplot as plt
import numpy as np
from scipy import signal
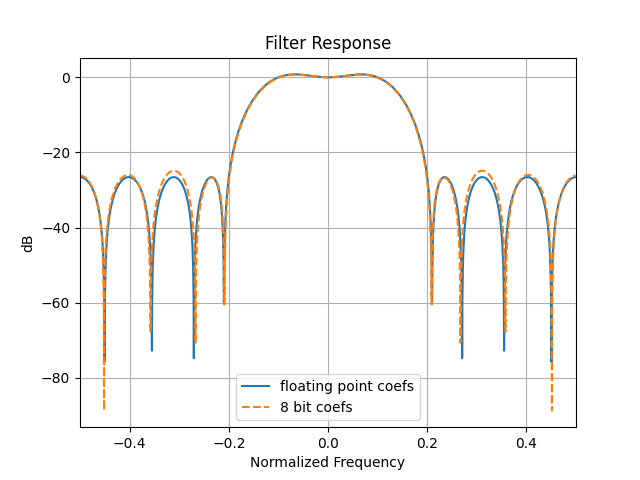
cutoff = .1 # Desired passband bandwidth, Hz
trans_width = .1 # Width of transition from pass to stop, Hz
numtaps = 13 # Size of the FIR filter.
fs = 1 # normalized sampling rate
# floating point coefficients
filter_coefs = signal.remez(numtaps, [0, cutoff, cutoff + trans_width, 0.5*fs],[1, 0], fs=fs)
# 8 bit integer coefficients
filter_coefs_int = np.round(filter_coefs * (2**7-1))
nfft = 2000;
print(filter_coefs_int)
x_fft = np.fft.fftshift(20*np.log10(np.abs(np.fft.fft(filter_coefs/np.sum(filter_coefs), nfft))))
xaxis = np.arange(-0.5, 0.5, 1/nfft)
x_fft_int = np.fft.fftshift(20*np.log10(np.abs(np.fft.fft(filter_coefs_int/np.sum(filter_coefs_int), nfft))))
plt.figure(3)
plt.plot(xaxis, x_fft)
plt.plot(xaxis, x_fft_int, linestyle='dashed')
plt.title('real portion of signal x')
plt.grid()
plt.xlabel('Normalized Frequency')
plt.ylabel('dB')
plt.title('Filter Response')
plt.xlim([-.5, .5])
plt.legend(['flating point coefs', '8 bit coefs'])
plt.show()
filter taps: [-1 -7 -4 4 18 32 38 32 18 4 -4 -7 -1]
Implement filter in verilog #
Lets implement our filter in verilog. This is not the best way (or even a good way) to design a filter in verilog, but it is a way to a implement a filter in verilog. Don’t get hung up on how incorrect or correct this is, we just want to demonstrate how to verify a complex system in cocotb.
fir.v #
module fir(clk, data_in, reset, data_out);
input clk;
input signed [7:0] data_in;
input reset;
output signed [15:0] data_out;
reg signed [15:0] data_out_reg;
// coefficients
wire signed [7:0] h0,h1,h2,h3,h4,h5,h6,h7,h8,h9,h10,h11,h12;
// multiplies
wire signed [15:0] m0,m1,m2,m3,m4,m5,m6,m7,m8,m9,m10,m11,m12;
// taps delays
wire signed [15:0] q1,q2,q3,q4,q5,q6,q7,q8,q9,q10,q11,q12;
// adders
wire signed [15:0] a1,a2,a3,a4,a5,a6,a7,a8,a9,a10,a11,a12;
// coefs from fir_design.py : [-1. -7. -4. 4. 18. 32. 38. 32. 18. 4. -4. -7. -1.]
// coeffs definition
assign h0 = -1;
assign h1 = -7;
assign h2 = -4;
assign h3 = 4;
assign h4 = 18;
assign h5 = 32;
assign h6 = 38;
assign h7 = 32;
assign h8 = 18;
assign h9 = 4;
assign h10 = -4;
assign h11 = -7;
assign h12 = -1;
// each multiply in the chain
assign m12 = h12 * data_in;
assign m11 = h11 * data_in;
assign m10 = h10 * data_in;
assign m9 = h9 * data_in;
assign m8 = h8 * data_in;
assign m7 = h7 * data_in;
assign m6 = h6 * data_in;
assign m5 = h5 * data_in;
assign m4 = h4 * data_in;
assign m3 = h3 * data_in;
assign m2 = h2 * data_in;
assign m1 = h1 * data_in;
assign m0 = h0 * data_in;
// each add in the chain
assign a1 = q1 + m11;
assign a2 = q2 + m10;
assign a3 = q3 + m9;
assign a4 = q4 + m8;
assign a5 = q5 + m7;
assign a6 = q6 + m6;
assign a7 = q7 + m5;
assign a8 = q8 + m4;
assign a9 = q9 + m3;
assign a10 = q10 + m2;
assign a11 = q11 + m1;
assign a12 = q12 + m0;
// delay line
dff dff1( .clk(clk), .reset(reset),.d(m12), .q(q1));
dff dff2( .clk(clk), .reset(reset),.d(a1), .q(q2));
dff dff3( .clk(clk), .reset(reset),.d(a2), .q(q3));
dff dff4( .clk(clk), .reset(reset),.d(a3), .q(q4));
dff dff5( .clk(clk), .reset(reset),.d(a4), .q(q5));
dff dff6( .clk(clk), .reset(reset),.d(a5), .q(q6));
dff dff7( .clk(clk), .reset(reset),.d(a6), .q(q7));
dff dff8( .clk(clk), .reset(reset),.d(a7), .q(q8));
dff dff9( .clk(clk), .reset(reset),.d(a8), .q(q9));
dff dff10(.clk(clk), .reset(reset),.d(a9), .q(q10));
dff dff11(.clk(clk), .reset(reset),.d(a10), .q(q11));
dff dff12(.clk(clk), .reset(reset),.d(a11), .q(q12));
// filter output data_out[n] = conv(x[n], h[n])
always @(posedge clk)
begin
if(reset)
data_out_reg <= 0;
else
data_out_reg <= a12;
end
assign data_out = data_out_reg;
// Dump waves
initial begin
$dumpfile("dump.vcd");
$dumpvars(1, fir);
end
endmodule
The above verilog uses another module, dff, so you will also need to include this in your design. This is a good example for showing how to include multiple verilog files in your cocotb makefile.
dff.v #
module dff(clk, reset, d, q);
input clk;
input reset;
input [15:0] d;
output [15:0] q;
reg [15:0] q_r;
always @(posedge clk or posedge reset)
begin
if(reset)
q_r <= 16'b0;
else
q_r <= d;
end
assign q = q_r;
endmodule
cocotb testbench #
testbench.py #
# Simple tests for an fir_filter module
import cocotb
import random
from cocotb.clock import Clock
from cocotb.triggers import Timer
from cocotb.triggers import RisingEdge
from scipy.signal import lfilter
import numpy as np
import matplotlib.pyplot as plt
# as a non-generator
def wave(amp, f, fs, clks):
clks = np.arange(0, clks)
sample = np.rint(amp*np.sin(2.0*np.pi*f/fs*clks))
return sample
def predictor(signal,coefs):
output = lfilter(coefs,1.0,signal)
return output
@cocotb.test()
async def filter_test(dut):
#initialize
dut.data_in.value = 0
fs = 1
amp0 = 80
num_clks = 512
nfft = num_clks;
f0 = 50*(1.0/nfft)
coefs = np.array([-1., -7., -4., 4., 18., 32., 38., 32., 18., 4., -4., -7., -1.])
cnt = 0
# input data
input_signal = wave(amp0, f0, fs,num_clks) + wave(amp0/2, 200.5*(1.0/nfft), fs, num_clks)
# bit accurate predictor values
data_out_pred = predictor(input_signal, coefs)
# start simulator clock
cocotb.start_soon(Clock(dut.clk, 1, units="ms").start())
# Reset DUT
dut.reset.value = 1
await RisingEdge(dut.clk)
dut.reset.value = 0
output_signal = np.zeros(num_clks)
# run through each clock
for samp in range(num_clks):
await RisingEdge(dut.clk)
# get the output at rising edge
dut_data_out = dut.data_out.value.signed_integer
# feed a new input in
dut.data_in.value = int(input_signal[samp])
output_signal[samp] = dut_data_out
# wait until reset is over, then start the assertion checking
if(cnt>=2):
assert dut_data_out == data_out_pred[cnt-2], "filter result is incorrect: %d != %d" % (dut_data_out, data_out_pred[cnt-2])
cnt = cnt + 1
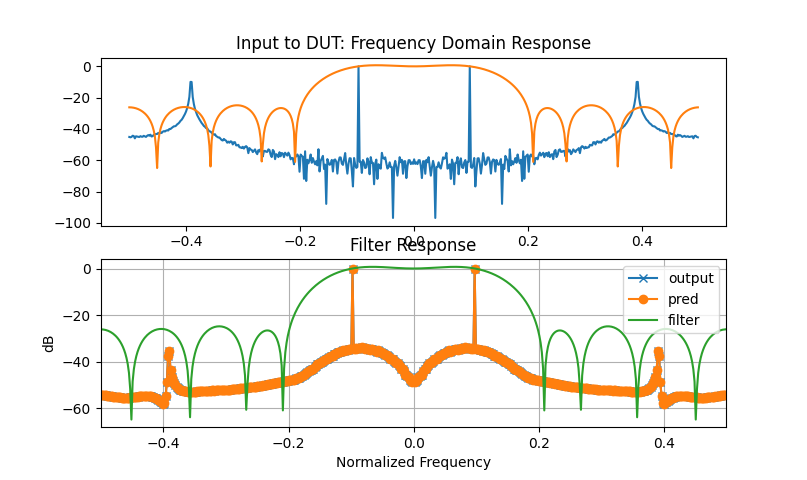
in_fft = np.fft.fftshift(20*np.log10(np.abs(np.fft.fft(input_signal, nfft))))
out_fft = np.fft.fftshift(20*np.log10(np.abs(np.fft.fft(output_signal[2:], nfft))))
pred_fft = np.fft.fftshift(20*np.log10(np.abs(np.fft.fft(data_out_pred[:-2], nfft))))
filt_fft = np.fft.fftshift(20*np.log10(np.abs(np.fft.fft(coefs/sum(coefs), nfft))))
# normalize FFTs lazy style
in_fft = in_fft - np.max(in_fft)
out_fft = out_fft - np.max(out_fft)
pred_fft = pred_fft - np.max(pred_fft)
xaxis = np.arange(-0.5, 0.5, 1/nfft)
plt.figure(1)
plt.subplot(1,2,1)
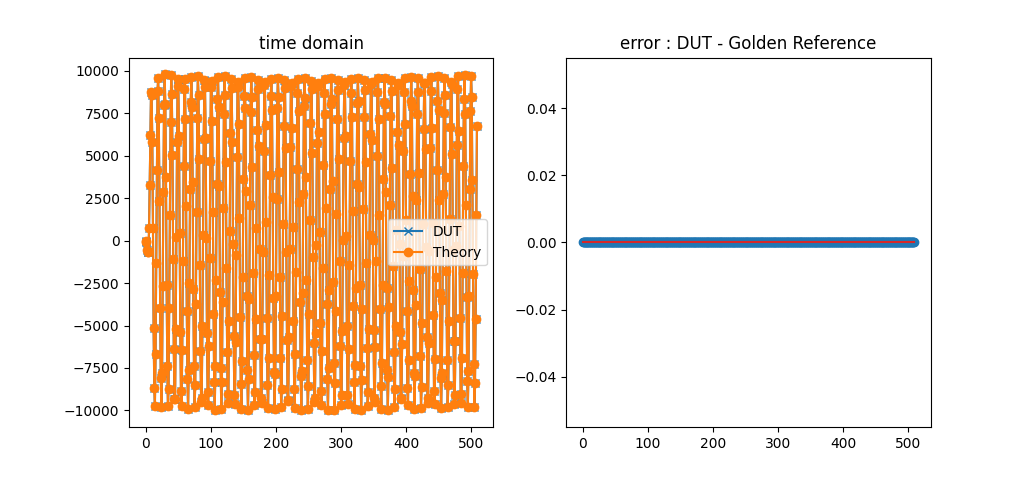
plt.plot(output_signal[2:], marker='x')
plt.plot(data_out_pred[:-2], marker='o')
plt.legend(['DUT', 'Theory'])
plt.title('time domain')
plt.subplot(1,2,2)
plt.stem(output_signal[2:]-data_out_pred[:-2])
plt.title('error : DUT - Golden Reference')
plt.figure(2)
plt.subplot(2,1,1)
plt.plot( xaxis, in_fft)
plt.plot(xaxis, filt_fft)
plt.title('Input to DUT: Frequency Domain Response')
plt.subplot(2,1,2)
plt.plot(xaxis, out_fft, marker='x')
plt.plot(xaxis, pred_fft, marker='o')
plt.title('Output of DUT: Frequency Domain Response')
plt.plot(xaxis, filt_fft)
plt.grid()
plt.xlabel('Normalized Frequency')
plt.ylabel('dB')
plt.title('Filter Response')
plt.xlim([-.5, .5])
plt.legend(['output', 'pred', 'filter'])
plt.show()
makefile #
# defaults
SIM ?= icarus
TOPLEVEL_LANG ?= verilog
VERILOG_SOURCES = $(PWD)/*.v
# use VHDL_SOURCES for VHDL files
# TOPLEVEL is the name of the toplevel module in your Verilog or VHDL file
TOPLEVEL = fir
# MODULE is the basename of the Python test file
MODULE = testbench
COCOTB_HDL_TIMEUNIT = 1ns
COCOTB_HDL_TIMEPRECISION = 1ps
# include cocotb's make rules to take care of the simulator setup
include $(shell cocotb-config --makefiles)/Makefile.sim
results #
Frequency Domain Plots:
Time Domain Plots:
Regression/Assertion Checks: